Home | Projects | Notes > Computer Architecture & Organization > ARM Instruction Set Architecture (ISA) - Data Processing Instructions

ARM Instruction Set Architecture (ISA) - Data Processing Instructions

ARM Data-processing Instructions

• Data-processing instructions are the instructions used to manipulate data not just move it from one location to another.

Arithmetic Instructions

Addition

• In most cases ADD is straightforward, but there are some cases that impact the processor and the instruction set.

  • Adding two binary numbers that fit into 32 bits works no problem!

    • On the ARM, the calculation will even set the Carry bit in the CCR if the results of bit 31 sum produces a carry.

    • 32 bits for positive or two's complement provides a good size range. If you do not need all the significant digits techniques can be used for larger (or smaller) numbers to lose accuracy but make for better speed.

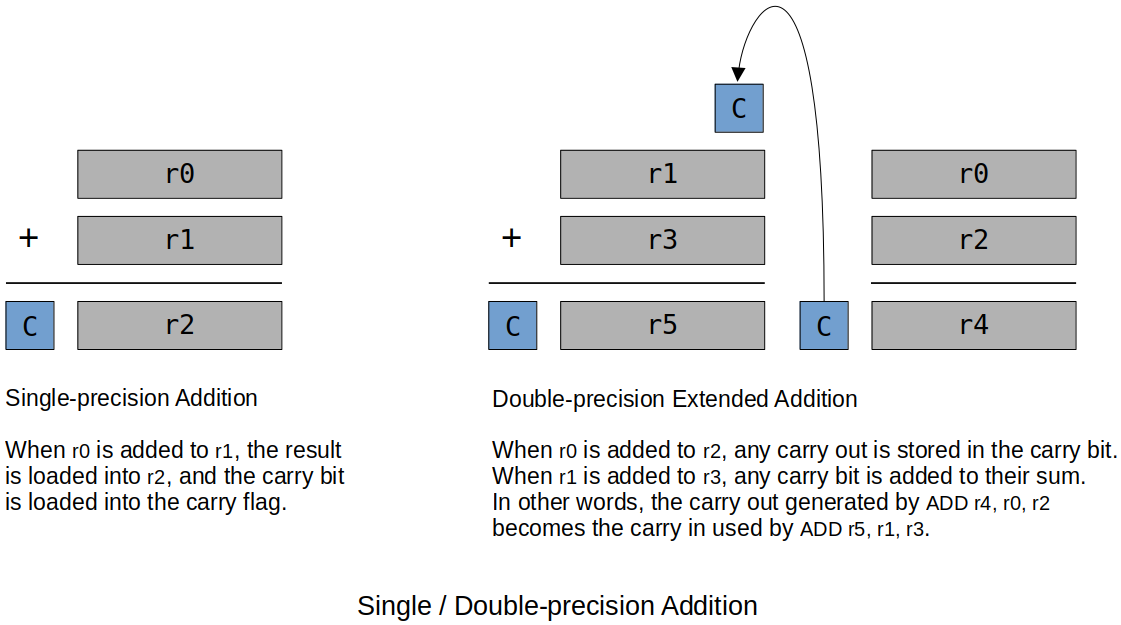
  • Adding two binary numbers that are too big to fit into 32 bits (e.g., 64-bit double or 128-bit quad word, etc.), can be problematic!

    • In this case, the assembly programmer has to handle this with register pairs since ARM can only add 32-bit words at a time.

      xxxxxxxxxx
      4
      1
      ADDS r4, r0, r2   @ Add the LSBs first and make sure the carry bit gets set.
      2
      ADDS r5, r1, r3   @ Add the MSBs and get the carry bit from the LSB add.
      3
         -
      4
         S is so carry bit gets set when necessary
      

      Using ADC(add with carry flag) in place of ADDS also works:

      xxxxxxxxxx
      2
      1
      ADC r4, r0, r2   
      2
      ADC r5, r1, r3  
      

Subtraction

• Normal subtraction

  xxxxxxxxxx
  1
  1
  SUB r1, r2, r3        @ RTL: [r1] ← [r2] - [r3]
  

• Reverse subtraction

  xxxxxxxxxx
  1
  1
  RSB r1, r2, r3        @ RTL: [r1] ← [r3] - [r2]
  

  This is necessary because in the literal addressing mode, the literal has to be the last operand. In this case you can't just switch the position of the operand to perform the reverse subtraction.

• Unlike addition, subtraction is NOT associative and NOT commutative.

  xxxxxxxxxx
  2
  1
  SUB r1, r2, #20       @ RTL: [r1] ← [r2] - 20
  2
  RSB r1, r2, #20       @ RTL: [r1] ← 20 - [r2]
  

  Above two operations do NOT yield the same result.

Negation

• Negation subtracts a number from zero.

• As ARM does not have a negation instruction, you as a programmer need to do the negation yourself by using reverse subtraction.

  xxxxxxxxxx
  2
  1
  RSB r1, r1, #0        @ Negates the contents of r1.
  2
                        @ if r1 originally contained 10, r1 becomes -10.
  

  In effect, RSB produces 2's complement.

  xxxxxxxxxx
  5
  1
  MVN r0, r1            @ Copies bitwise NOT of argument. In other words,
  2
                        @ copies the logical complement of the contents of r1.
  3
                        @            ------------------
  4
                        @            bit reversal!
  5
                        @            it's not sign reversal (arithmetic reversal)
  

  In effect, MVN produces 1's complement.

Comparison

• Implicit comparison (need to add S)

  • CCR bits set based on the ALU operation SUBS, ADDS, etc.

• Explicit comparison (always set the flags)

  • CCR bits set based on CMP or TST instruction.

Multiplication

• Since the multiplication of two n-bit operands may produce the product of size up to 2n-bits, this has to be handled with care.

1. If it is guaranteed that two operands and the product will all fit into 32 bits.

   xxxxxxxxxx
   14
   1
   MUL rd, rm, rs       @ RLT: [rd] ← [rm] * [rs]
   2
                        @
   3
                        @ Note that rd and rm cannot be the same, because in this 
   4
                        @ multiplication algorithm rd is used to build up the answer so if
   5
                        @ rd and rm are the same, the intermediate calculation gets 
   6
                        @ interfered.
   7
                        @ - MUL r0, r0, r1  @ NOT OK!
   8
                        @ - MUL r0, r1, r0  @ OK
   9
                        @ 
   10
                        @ The Raspberry Pi assembler checks for this and generates an
   11
                        @ error during assembly. 
   12
                        @ - I have personally observed this error caused by using 
   13
                        @ ADD r1, r1, r2. This was easily solved by just modifying the 
   14
                        @ code to ADD r1, r2, r1.
   

2. If the overflow is expected (or if you are not sure).

   xxxxxxxxxx
   17
   1
   UMULL rL, rU, rA, rB     @ RTL: [rU, rL] ← [rA] * [rB]
   2
                            @
   3
                            @ Multiply rA and rB, place 64-bit unsigned result
   4
                            @ into {rU, rL} 
   5
                            @       --  --
   6
                            @       |   least significant 32 bits
   7
                            @       |
   8
                            @       most significant 32 bits
   9
                            @       ------------------------
   10
                            @       if this part is 0, no overflow
   11
                            @
   12
                            @ UMULL interprets values from rA and rB as 
   13
                            @ unsigned integers.
   14
   
   15
   UMULLS rL, rU, rA, rB    @ If S is specified, 
   16
                            @ - update N and Z flags according to the result.
   17
                            @ - does not affect the C or V flags.
   

   The reason UMULL has to be used in this case is because MULLS will not set the CCR flags. (Because of how the MUL works there is no way to ensure the hardware can set flags correctly so it does NOTHING. The carry bits are tied to specific bits in the ALU. It is possible when a multiplication is performed, those specific bits can show no issues but there turns out to be overflow issues.

• Multiply and Accumulate (MLA)

  xxxxxxxxxx
  3
  1
  MLA r0, r1, r2, r3        @ RTL: [r0] ← [r1] * [r2] + [r3]
  2
                            @ Does the multiplication and adds the product to
  3
                            @ the running total.
  

Division

• ARM does not have instruction for division.

• Same type of problem with multiplication occurs in division.

• There is a quotient, remainder and the sign that has to be handled as well.

• You as a programmer have to write the division subroutine yourself.

  • Works best as a loop that does repeated subraction until you can no longer subtract the whole number, producing a quotient and a remainder.

  • See Multiplication & Division for more details.

Bitwise Logical Operations

• Bitwise logical operations are apply to the individual bits of a register.

• AND, ORR, EOR

  xxxxxxxxxx
  6
  1
      0100              0100              0100
  2
  AND 1111          ORR 1111          EOR 1111
  3
  --------          --------          --------
  4
      0100              1111              1011
  5
  
  6
  Bitwise AND       Bitwise OR        Bitwise exclusive OR (XOR)
  

• NOT is not supported by ARM. But, you can implement it by:

  • Using EOR with #FFFFFFFF on one register.

  • Using the MVN instruction. (See Negation section above for more details about NVM.)

• BIC (Bit Clear)

  • AND's the first operand with the logical complement of the second.

    xxxxxxxxxx
    3
    1
    BIC r1, r2            @ RTL: [r1] ← [r1] · [r2]
    2
                                             ^
    3
                                            AND
    

  • Can be used to clear out the low-order byte of a register.

    xxxxxxxxxx
    2
    1
    BIC r0, r1, #0xFF     @ Copies the 32 bits in r1 to r0 then clears bits 0 to 7 of 
    2
                          @ the data in r0.
    

• A mask is used with a specific logical operation to get the bit we want to know about and exclude the ones we do not care about.

Shift Operations

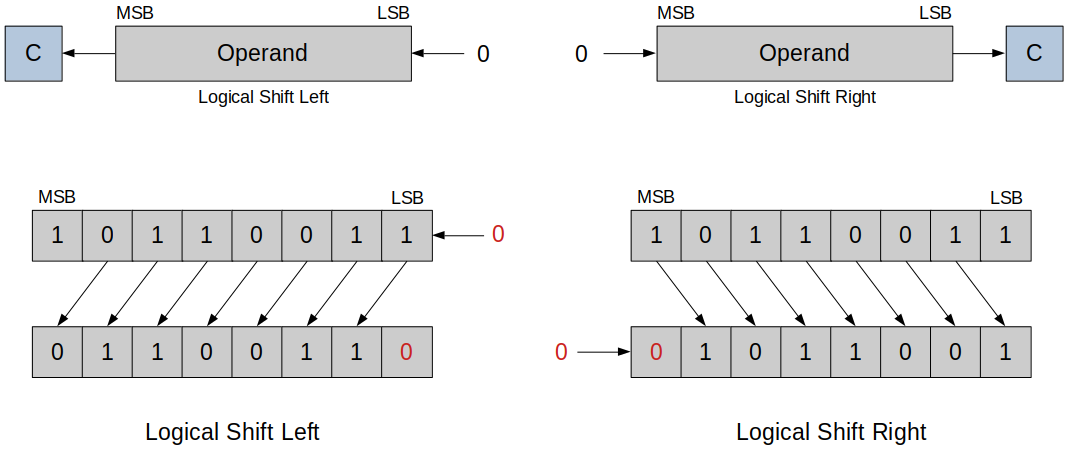
• Logical shift

  • Logical Shift Left

    • Each bit is shifted towards left, MSB is discarded and LSB becomes 0.

  • Logical Shift Right

    • Each bit is shifted towards right, LSB is discarded and MSB becomes 0.

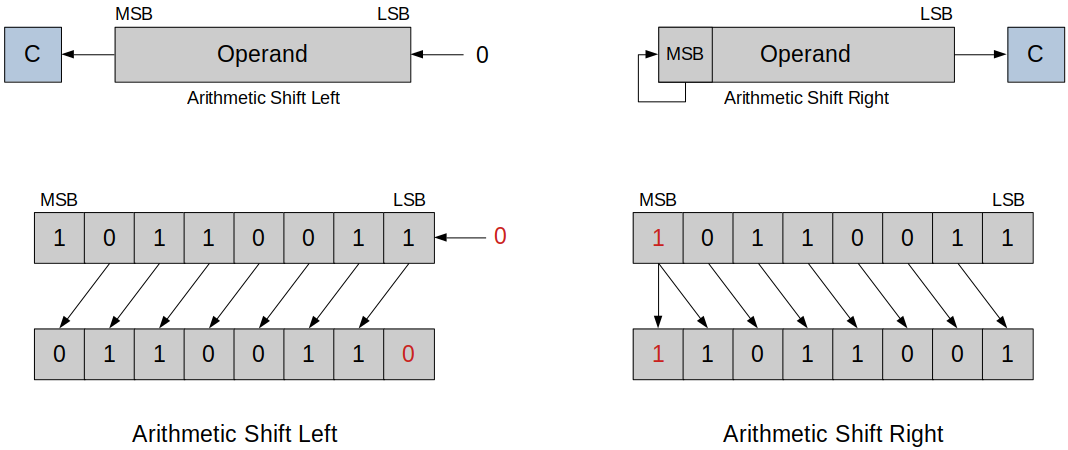
• Arithmetic shift

  • Arithmetic Shift Left

    • Each bit is shifted towards left, MSB is discarded and LSB becomes 0. (Similar to logical shift)

      • In this example, the operation has overflowed. Meaning, the result of the multiplication is larger than the largest possible value.

  • Arithmetic Shift Right

    • Each bit is shifted towards right, LSB is discarded and MSB is preserved.

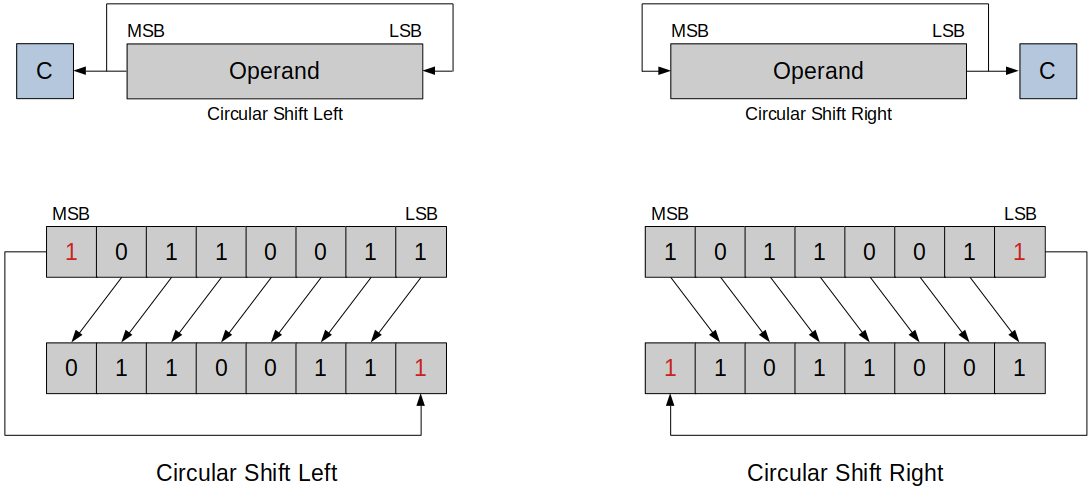
• Circular shift (Rotate)

  • The bit shifted out is copied into the bit vacated at the other end (i.e., no bit is lost during a rotate).

  • The bit shifted out is also copied into the carry bit.

  • Following figure shows ROL and ROR.

• Implementing a Shift Operation on the ARM

  • ARM's implementation of shift operations is unique in that there is no explicit shift operations.

    • Instead, shifting is combined with other data processing operations because the second operand can be shifted before it is used.

  • ARM has a barrel shifter that can be applied to the second operand of almost any instruction.

  • A barrel shifter uses combinational logic to perform the shift without shift registers.

    • With rsource2 and shift control information, the barrel shifter knows exactly what to do.

    • This allows multiple bits to be shifted in one execution cycle instead of each bit being shifted in each execution cycle.

• ARM implements only the following five shifts (the programmer must synthesize the rest).

  xxxxxxxxxx
  5
  1
  LSL   logical shift left
  2
  LSR   logical shift right
  3
  ASR   arithmetic shift right
  4
  ROR   rotate right
  5
  RRX   rotate right through the carry (only one bit at a time)
  

  Don't be confused! These are operators NOT instructions.

  Since ARM does not have shift instructions, you, as a programmer, need to from instructions by using these operators as arguments to perform shift. For example:

  xxxxxxxxxx
  3
  1
  MOV r1, r1, LSL #1    @ shifts r1's bits one bit-place to the left
  2
              ---
  3
              used as an "argument"