Home | Projects | Notes > Computer Architecture & Organization > Floating-Point Arithmetic

Floating-Point Arithmetic

Floating-Point Arithmetic

Multiplication

• Consider an example using a 8-bit significand and an unbiased exponent with

  xxxxxxxxxx
  2
  1
  A = 1.0101001 x 2^4   
  2
  B = 1.1001100 x 2^3     
  

  To multiply these number you multiply the significands and the exponents.

  xxxxxxxxxx
  4
  1
  A x B = (1.0101001 x 2^4) x (1.1001100 x 2^3)    
  2
        = (1.0101001 x 1.1001100) x 2^(4+3)
  3
        = 10.00011010101100 x 2^7
  4
        = 1.000011010101100 x 2^8
  

Addition

• Consider an example using a 8-bit significand and an unbiased exponent with

  xxxxxxxxxx
  2
  1
  A = 1.0101001 x 2^4   
  2
  B = 1.1001100 x 2^3     
  

  If these two floating-point numbrs were to be added by hand, we would automatically align the binary points of A and B as follows.

  xxxxxxxxxx
  4
  1
     10101.001
  2
  +)  1100.1100
  3
  -------------
  4
    100001.1110
  

  However, as these numbers are held in a normalized floating-point format, the computer has the following problem of adding

  xxxxxxxxxx
  3
  1
     1.0101001 x 2^4   
  2
  +) 1.1001100 x 2^3     
  3
  ------------------
  

  The Computer has to carry out the following steps to equalize exponents.

  xxxxxxxxxx
  6
  1
  Step 1.   Identify the number with the smaller exponent.
  2
  Step 2.   Make the smaller exponent equal to the larger exponent by dividing 
  3
            the significand of the smaller number by the same factor by which 
  4
            its exponent was increased.
  5
  Step 3.   Add (or subtract) the significands.
  6
  Step 4.   If necessary, normalize the result (post normalization).
  

  We can now add A to the denormalized B.

  xxxxxxxxxx
  6
  1
     1.0101001 x 2^4   
  2
  +) 0.1100110 x 2^4     
  3
  ------------------
  4
    10.0001111 x 2^4
  5
  
  6
  Normalized sum: 1.00001111 x 2^5
  

Rounding and Truncation Errors

• Because floating-point arithmetic can lead to an increase in the number of bits in the significand, you need a means of keeping the number of bits in the significand constant.

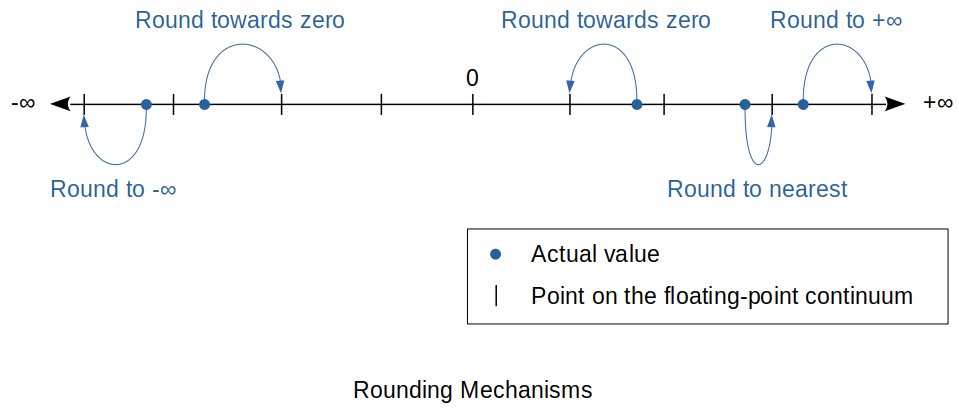
• Truncation

  • Simplest technique.

  • a.k.a. Rounding towards zero since it makes a negative number larger and a positive number smaller.

• Rounding to nearest

  • The closest floating-point representation to the actual number is used.

  • Preferred method of all because it is more accurate and gives an unbiased error. (Result can be smaller or larger so they even out.)

• Rounding to positive/negative infinity

  • The nearest valid floating-point number in the direction of positive infinity or negative infinity respectively is chosen.

• When the number to be rounded is midway between two points on the floating-point continuum, IEEE rounding specifies the point whose least-significant digit is zero (i.e., round to even).