Home | Projects | Notes > Computer Architecture & Organization > Floating-Point Numbers

Floating-Point Numbers

Floating-Point Notation

• A floating-point value is stored as two components:

  • A number

  • The location of the radix (In base 10 it is called the decimal) point within the number.

• Floating-point arithmetic lets you handle the very large and very small number found in scientific applications.

Binary Floating-Point Number

• The term mantissa has been replaced by significand to indicate the number of significant bits in a floating-point number.

• Example:

  • ${101010.111110}_{(2)}$$101010.111110_{(2)}$ can be represented by $1.01010111110\times 2^5$$1.01010111110 \times 2^5$

    • Significand: $1.01010111110$$1.01010111110$

    • Exponenet: $5$$5$ ($00000101$$00000101$ in 8-bit binary arithmetic)

• Because a floating-point number is defined as the product of two values, a floating point expression is not unique;

  • e.g., $10.110\times 2^4=1.011\times 2^5$$10.110 \times 2^4 = 1.011 \times 2^5$

Normalization of Floating-Point Numbers

• An IEEE-754 floating-point significand is always normalized (unless it is equal to zero).

  • $1.000...0\times 2^e\le \text{significand}\le 1.111...1\times 2^e$$1.000...0 \times 2^e ≤ \text{significand} ≤ 1.111...1 \times 2^e$

  • Significand always begins with a leading $1$$1$.

• Normalization allows the highest available precision by using all significant bits.

  • e.g., $0.0000101$$0.0000101$ has only three significant bits, whereas the normalized 8-bit significand $1.0100011$$1.0100011$ has eight significant bits.

• Examples:

  • $0.110...\times 2^e$$0.110... \times 2^e$ would be normalized to $1.10...\times 2^{e-1}$$1.10... \times 2^{e-1}$

  • $10.1...\times 2^e$$10.1... \times 2^e$ would be normalized to $1.01...\times 2^{e+1}$$1.01... \times 2^{e+1}$

Biased Exponents

• The significand of an IEEE format floating-point number is represented in sign and magnitude form. (A sign-bit indicates positive or negative)

• The exponent is represented in a biased form, by adding a constant called a biase to the true exponent.

  • This is to make the range of the exponent nonnegative.

• Examples: Suppose an 8-bit exponent is used and all exponents are biased by $127$$127$.

  • $1010.1111$$1010.1111$ is normalized to $+1.01011111\times 2^3$$+1.01011111 \times 2^3$. Here, true exponent is $+3$$+3$ and the biased exponent $3+127=130$$3 + 127 = 130$ ($10000010$$10000010$ in binary form) will be stored.

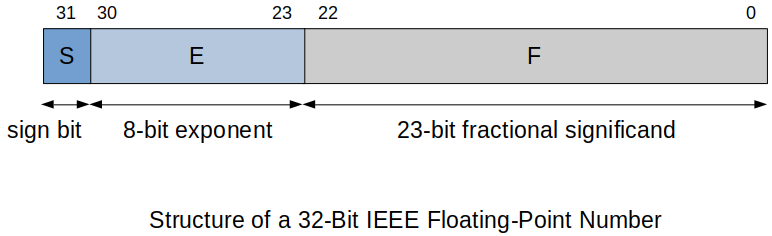
IEEE Floating-Point Numbers

• IEEE-754 floating-point in 32-bit uses the following format:

  xxxxxxxxxx
  1
  1
  S EEEEEEEE 1.MMMMMMMMMMMMMMMMMMMMMMM
  

  • S: Sign bit (1-bit)

  • E: 8-bit biased exponent (tells you where to put the binary point)

    • The stored exponent value $0$$0$ (true: $-127$$-127$), and $255$$255$ (true: $128$$128$) are used to indicate special values, so the exponential range of this format is restricted to: (For 32-bits)

      • Binary range: $2^{-126}$$2^{-126}$ to $2^{127}$$2^{127}$

      • Decimal range: ${10}^{-45}$$10^{-45}$ to ${10}^{38}$$10^{38}$

  • M: 23-bit fractional significand.

    • Leading $1$$1$ and decimal point are not stored in memory because they do not change. (This is why this part is called the fractional significand.)

• IEEE-754 floating-point in 32-bit can represent 2³² = 4,294,967,296 different numbers. These include:

  • The number 0.0

    • sign: 0, exponent: 0, mantissa: 0

  • ±∞

  • Very small denormalized numbers

  • Various other special conditions

• Overall, the standard allows approximately seven significant decimal digits and and approximate value range of 10^-45 to 10³⁸.

• IEEE-754 floating-point in 32-bit is still very limited to express the infinite number of real numbers in reality. For this reason, followings are defined as well.

  • For 64-bit

    • 16 significant decimal digits

    • Decimal range: 10^-300 to 10³⁰⁰

  • For 128-bit

    • Decimal range: 10^-4900 to 10⁴⁹⁰⁰

    • 34 decimal digits

  [!] Note: There is a 16-bit format which is extremely limited in both range and precision, but is useful for simple graphics applications.

Example of Decimal to Binary Floating-Point Conversion

• Converting 253.75(10) to binary floating-point form.

  xxxxxxxxxx
  24
  1
  Step 1. Convert 253 and 0.75 to hex first, then to binary.
  2
  
  3
          253 = FD (hex), 1111 1101 (binary)
  4
          16 * 0.75 = 12.0, 0.C (hex), 0.1100 (binary)
  5
          ∴ 253.75 (decimal) = FD.C (hex) = 1111 1101 . 1100 (binary)
  6
  
  7
  Step 2. Normalize.
  8
  
  9
          1.111 1101 1100 x 2^7
  10
  
  11
  Step 3. Get the exponent.
  12
  
  13
          7 + 127 = 134 = 1000 0110 (binary)
  14
  
  15
  Step 4. Put the parts together to form the floating-point format.
  16
  
  17
          S  EEEE EEEE  1.MMMMMMMMMMMMMMMMMMMMMMM
  18
          0  1000 0110    11111011100000000000000   (Do not copy '1.')
  19
  
  20
  Step 5. Regroup this by 4's and convert into hex. (For easy grading!)
  21
   
  22
          0100 0011 0111 1101 1100 0000 0000 0000
  23
          
  24
          ∴ 437DC000 (hex)
  

Example of Binary Floating-Point to Decimal Conversion

• Do the previous example in reverse order!

• Just don't forget:

  • The implied "1." in mantissa

  • The exponent is in biased form