Home | Projects | Notes > Computer Architecture & Organization > Sequential Circuits

Sequential Circuits

Combinational Circuits vs. Sequential Circuits

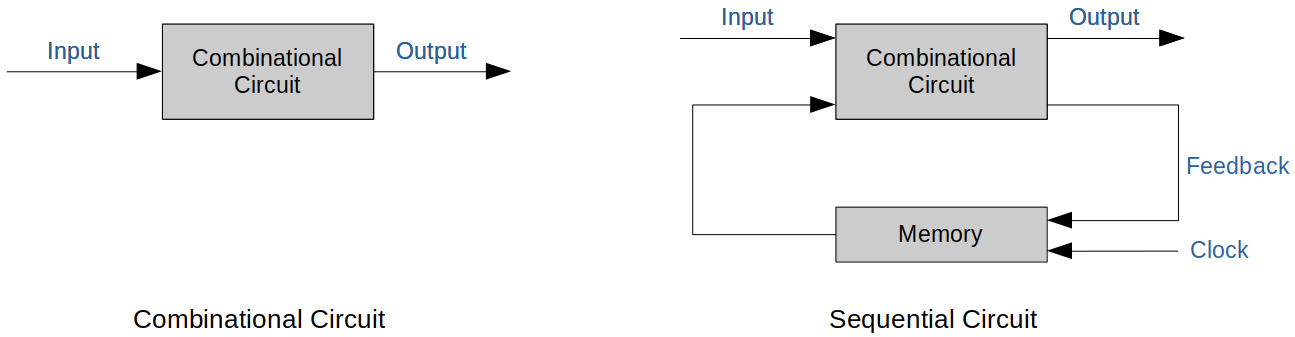
• Combinational circuits

  • Outputs determined ONLY by its input(s).

• Sequential circuits

  • Outputs determined by its input(s) and its previous state.

  • Basically a combinational circuit combined with a memory element. Memory element could be:

    • Latches - clock (X), therefore asynchronous

    • Flip-flops - clock (O), therefore synchronous

SR Latch (NOR)

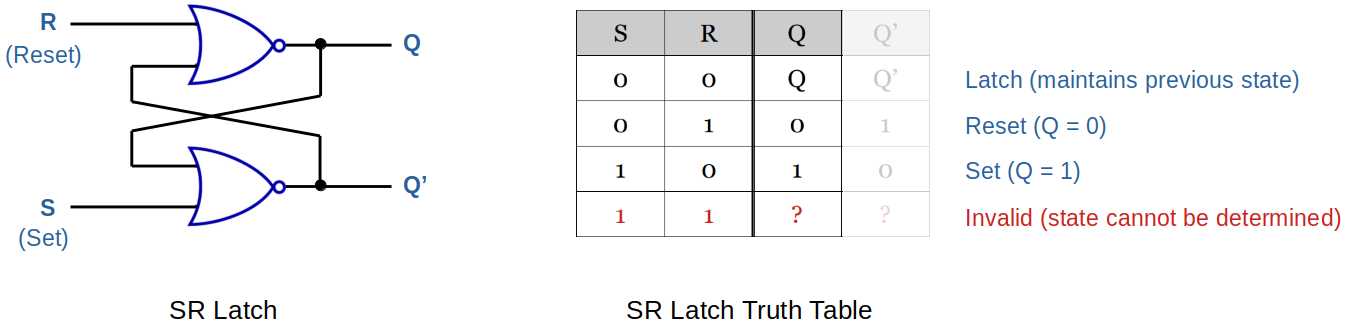
• An SR latch (Set/Reset) is an asynchronous device.

• Relies only on the state of the S and R inputs.

• Following is an SR latch created with two NOR gates that have a cross-feedback loop.

  • Can also be made from NAND gates, but the inputs are swapped and negated.

Clocked SR Flip-Flop (AND-NOR)

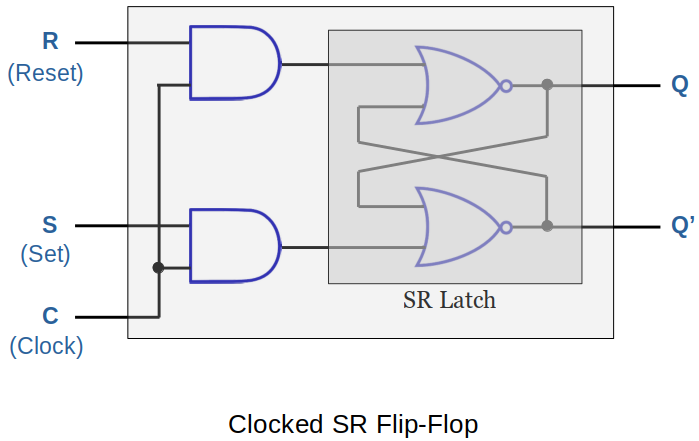
• An SR flip-flop is a synchronous device.

• Following SR filp-flop is built from a pair of AND gates added to a basic SR latch made from NOR gates.

• Analysis

  • When (clock) signal stays 0, the flip-flop maintains the previous state. (∵ Two AND gates are disabled.)

  • When C stays 1, the filp-flop behaves like the standard SR latch.

D (Data) Flip-Flop

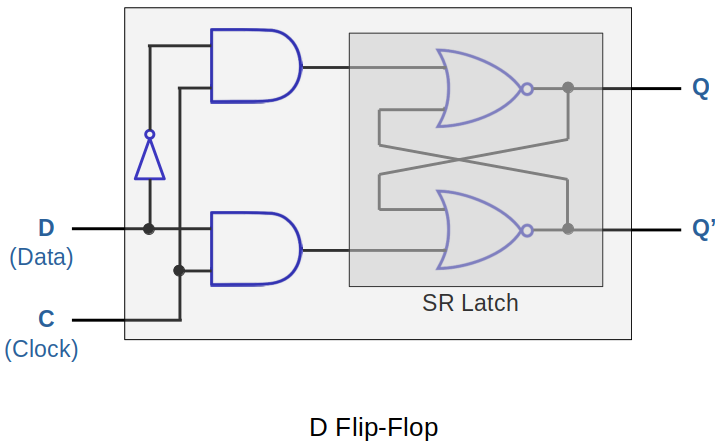
• Why can't we just tell it what we want to store and not worry about S and R values? (So, we have D flop-flop!)

• Analysis

  • The D flip-flop captures the value of the D-input at a definite portion of the clock cycle (such as the rising edge of the clock). That captured value becomes the Q-output.

  • At other times, the output-Q maintains the previous value.

Registers

• A register is a group of flip-flops which share a common clock.

  • An $n$$n$-bit register is made from $n$$n$ flip-flops. (Capable of storing $n$$n$-bits of information.)

  • May have additional logic to allow for other functions.

4-Bit Register with Parallel Load

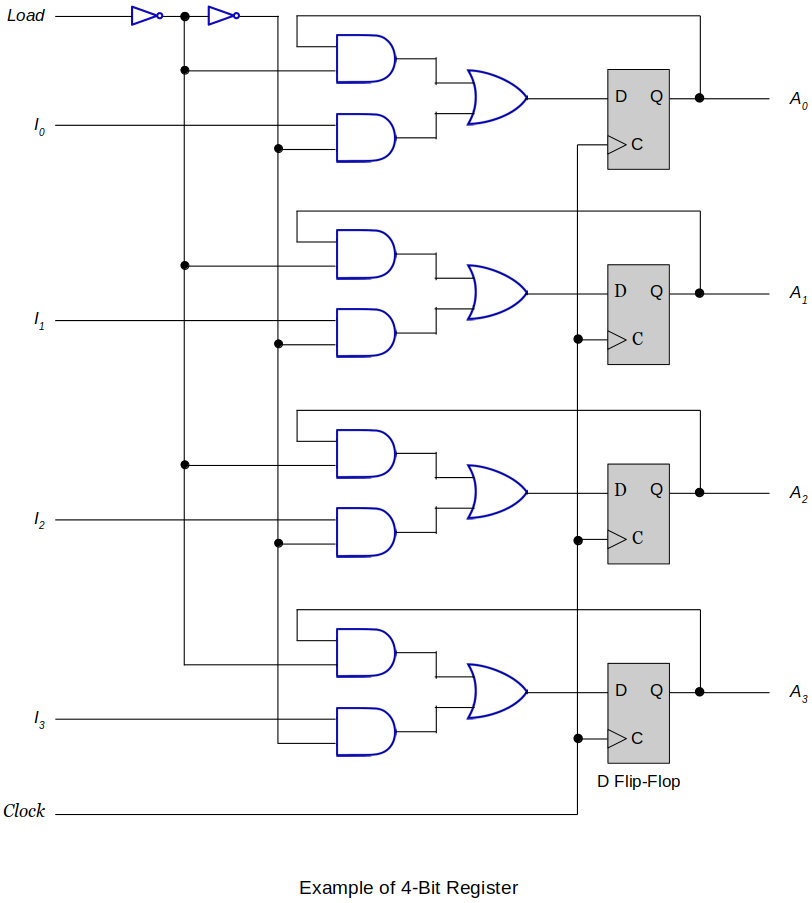
• When Load = 1

  • The lower of the each AND gate pair will be enabled, and the upper AND gates will be disabled.

  • The values I0 ~ I3 will then be stored into the flip-flops at a definite portion of the clock cycle (such as the rising edge of the clock.)

• When Load = 0

  • The upper of the each AND gate pair will be enabled, and the lower AND gates will be disabled.

  • The values stored in each D filp-flop will remain unchanged due to the feedback loop.

4-Bit Register with Parallel Load (Improved Design with Fewer Gates)

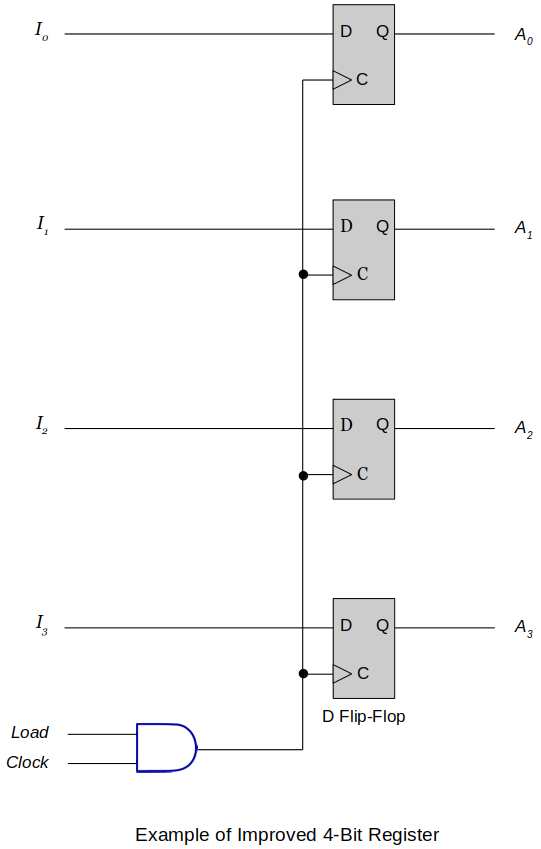
• How you can keep the D flip-flops from changing the values when you don't want them to change with fewer gates?

  • Introduce an AND gate into the clock path!

Shift Registers

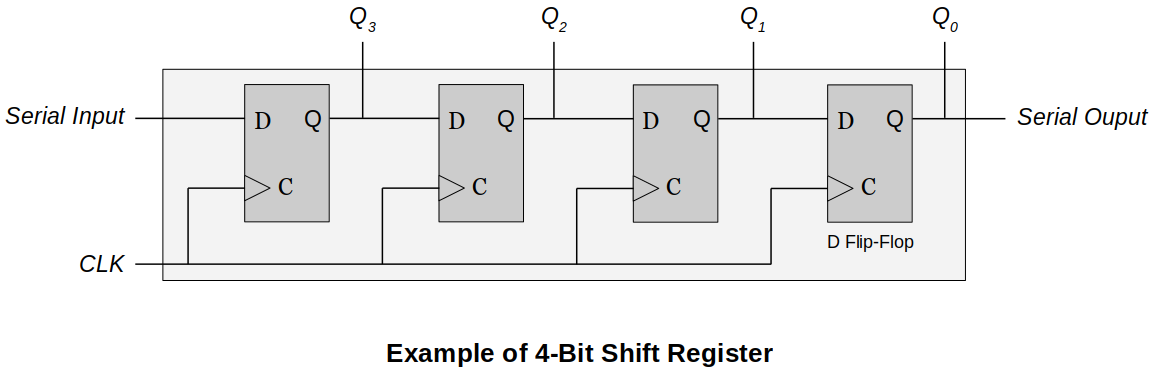
• A shift register moves the bits stored in it one or more positions to the right or left.

  • Moving to the right divides the binary number by 2.

  • Moving to the left multiplies the binary number by 2.

• In the following example, four clock cycle will be required to completely load a 4-bit data.

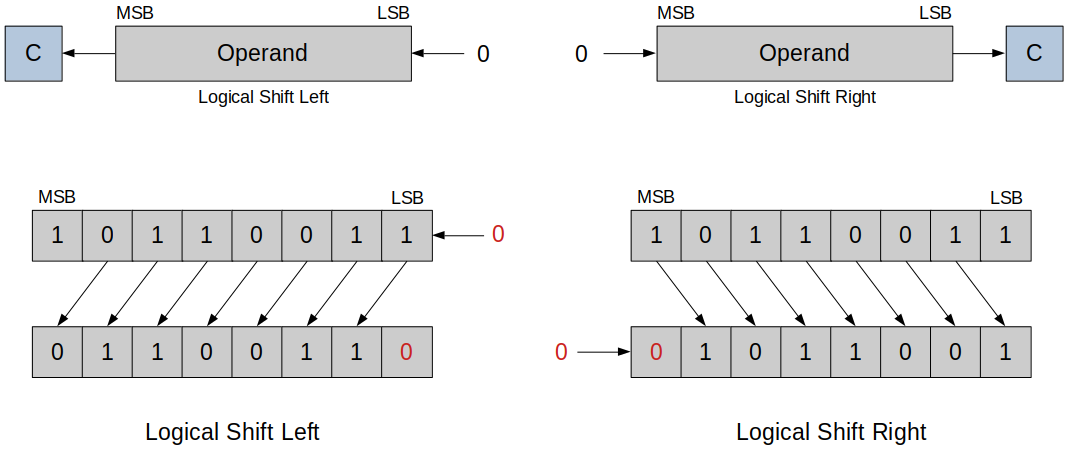
• Logical shift

  • Logical Shift Left

    • Each bit is shifted towards left, MSB is discarded and LSB becomes 0.

  • Logical Shift Right

    • Each bit is shifted towards right, LSB is discarded and MSB becomes 0.

• Arithmetic shift

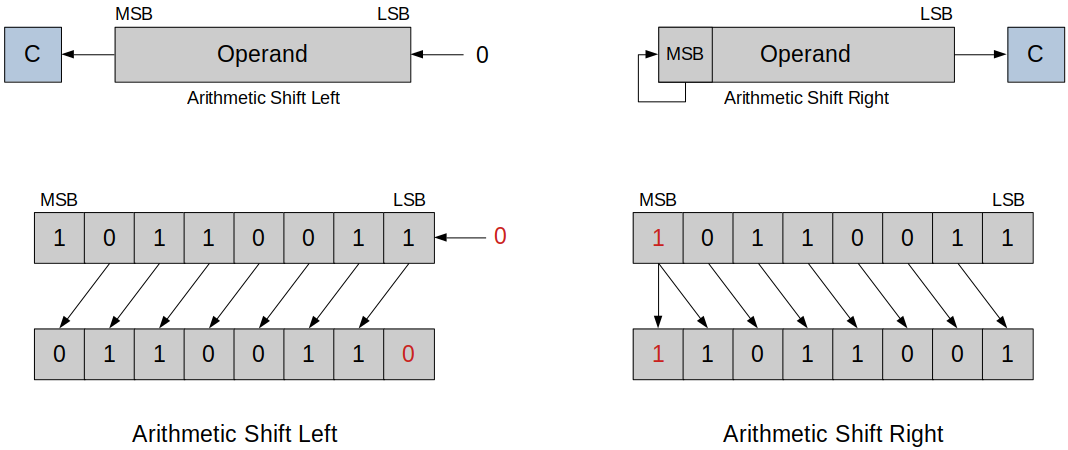
  • Arithmetic Shift Left

    • Each bit is shifted towards left, MSB is discarded and LSB becomes 0. (Similar to logical shift)

      • In this example, the operation has overflowed. Meaning, the result of the multiplication is larger than the largest possible value.

  • Arithmetic Shift Right

    • Each bit is shifted towards right, LSB is discarded and MSB is preserved.

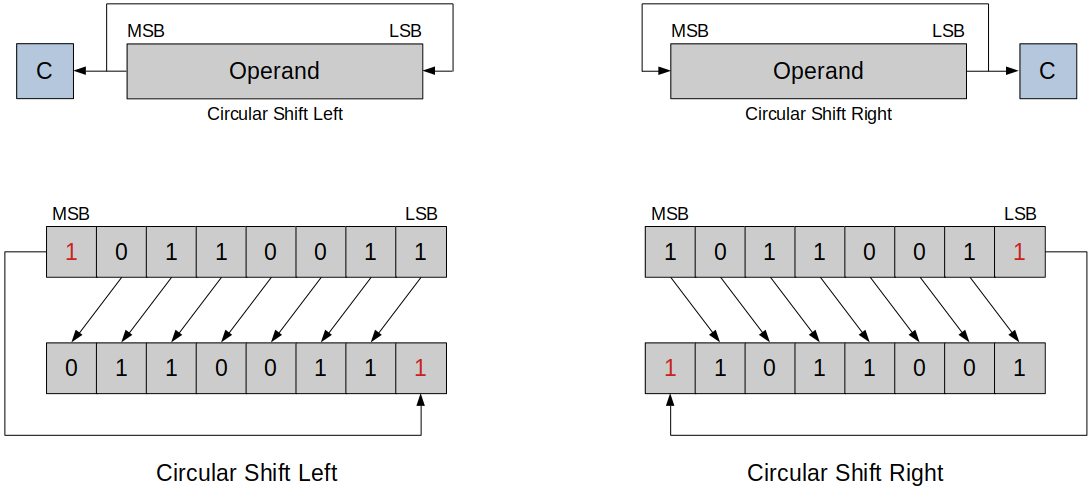
• Circular shift

  • The bit that would be lost is moved into the register.

Applications of Shift Registers

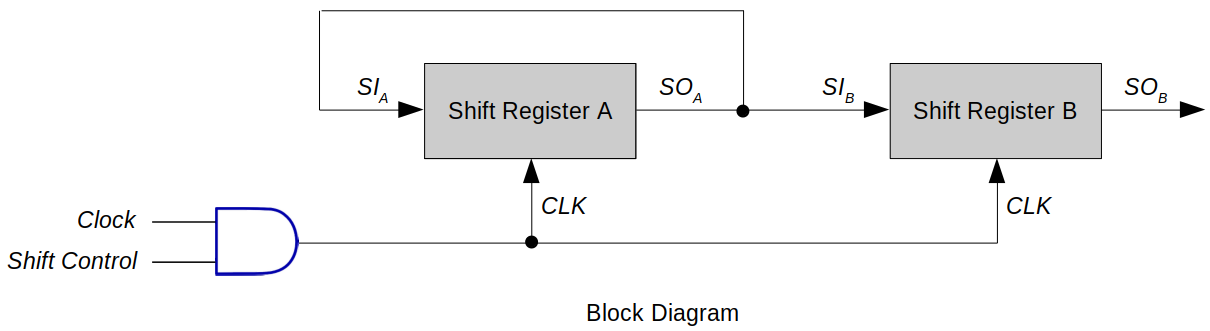
Serial Transfer from One Register to Another

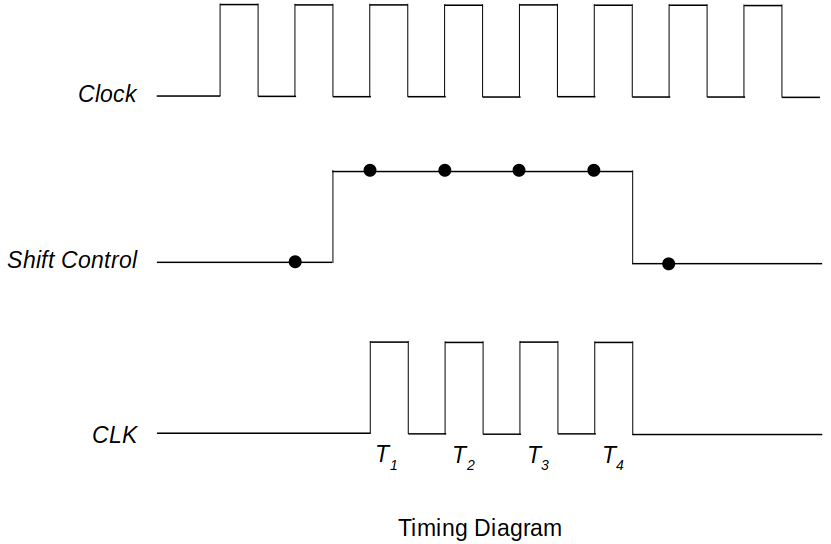
• Following example demonstrates a serial transfer of a 4-bit data from one register to another.

  • It will take exactly four clock cycles for the contents stored in A to be completely transferred to B.

  • When shift control is high, at each clock pulse, one bit at a time is copied from A to B.

  • The feedback formed by SO_A and SI_A helps A retain its value after the completion of the data transfer.

• This circuit is easy to build and cheap, but not fast.

Serial Adder

• Following example demonstrates A = A + B operation where the sum of A and B gets stored into A. (A's original value is overwritten.)

  • D flip-flop holds the carry of the previous sum and when an appropriate clock cycle hits this carry will be transferred into the full adder to be added with new x and y.

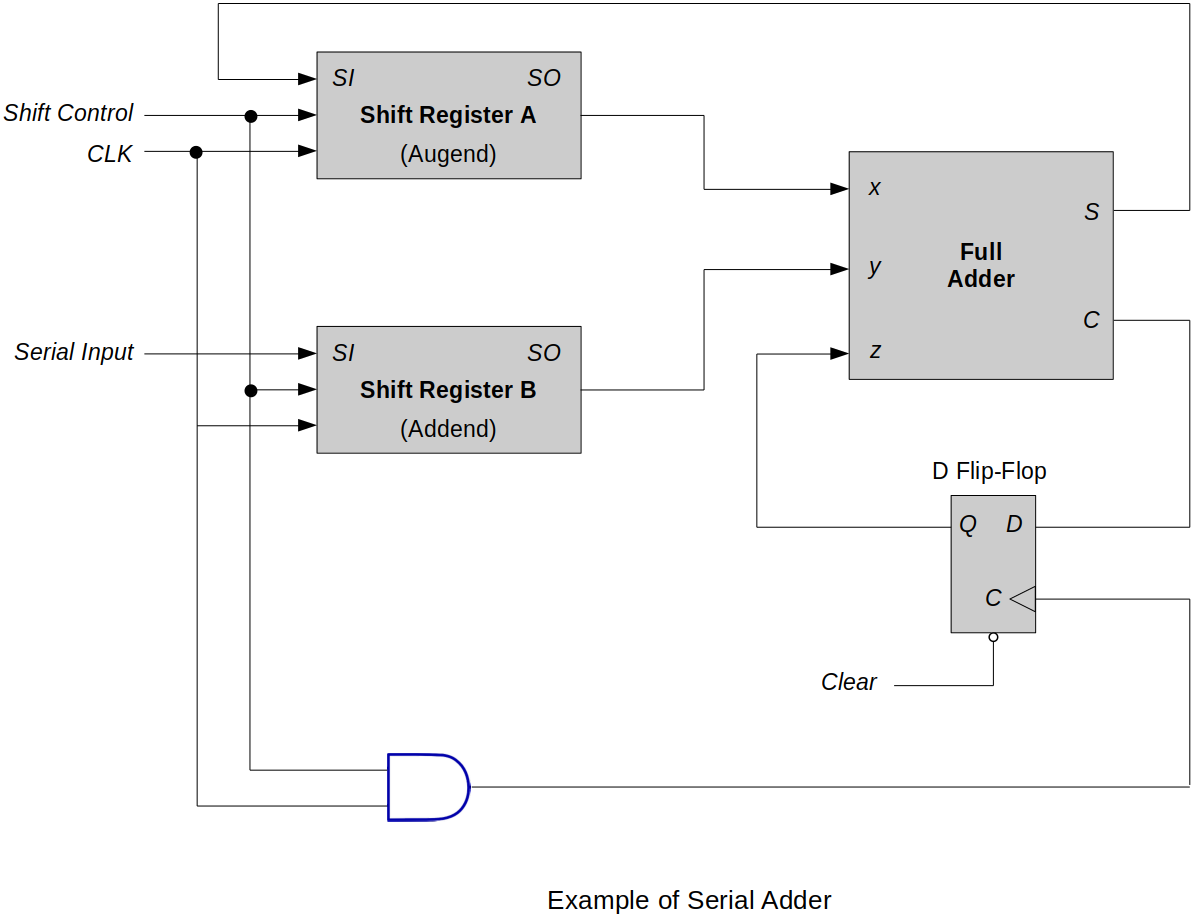
• One problem with this circuit is that B won't retain its value after the operation, which is far from how modern computer systems handle this.

  • Some improvements can be made to make this circuit more functional.

    • Make Shift Register B a circular shift register so that it retains its original value after the operation.

    • Add another register so that the circuit performs C = A + B.