Home | Projects | Notes > Data Structures & Algorithms > Binary Search Trees (BST)

Binary Search Trees (BST)

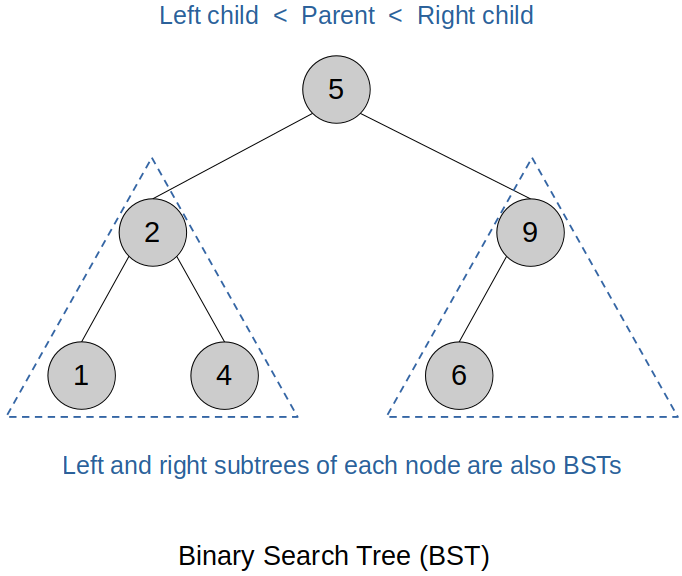
Introduction

A Binary Search Tree (BST) is a type of binary tree where each node follows a specific ordering rule:

• The left subtree contains only nodes with values less than the parent node.

• The right subtree contains only nodes with values greater than the parent node.

• This rule applies recursively to every subtree in the tree.

BSTs are widely used for efficient searching, insertion, and deletion, with average-case time complexity of O(log n) for balanced trees.

• All operations have O(log n) time complexity, which is very efficient. (Every time you go down one level, you are excluding the half of the remaining nodes from your search.)

  $\to$$\to$ Divide and conquer!

• If a tree never forks, it is essentially a linked list, in which case the search time complexity will be O(n). However, since this is not a general case, a binary search tree is still treated as an O(log n) data structure.

Implementation (C++): Non-Recursive

Header (bstree.hpp)

31
1
#ifndef BSTREE_HPP
2
#define BSTREE_HPP
3

4
class node 
5
{
6
public:
7
    node (const int val) : data(val), p_left(nullptr), p_right(nullptr) {}
8

9
    int data;
10
    node *p_left;
11
    node *p_right;
12
};
13

14
class bstree
15
{
16
public:
17
    bstree() : p_root(nullptr) {}
18
    ~bstree() { clear(); }
19
    bool insert(const int val);
20
    bool search(const int val) const;
21
    void preorder() const;
22
    void inorder() const;
23
    void postorder() const;
24
    bool remove(const int val);
25
    void clear();
26

27
private:
28
    node *p_root;
29
};
30

31
#endif

Source (bstree.cpp)

282
1
#include "bstree.hpp"
2
#include <iostream>
3
#include <stack>
4

5
bool bstree::insert(const int val)
6
{
7
    node *p_new = new node(val);
8

9
    // inserting into an empty BST
10
    if (p_root == nullptr)
11
    {
12
        p_root = p_new;
13
        return true;
14
    }
15

16
    node *p_curr = p_root;
17

18
    while (true)
19
    {
20
        if (val < p_curr->data)
21
        {
22
            if (p_curr->p_left == nullptr)
23
            {
24
                // insert
25
                p_curr->p_left = p_new;
26
                return true;
27
            }
28
            else
29
            {
30
                // keep searching
31
                p_curr = p_curr->p_left;
32
            }
33
        }
34
        else if (val > p_curr->data)
35
        {
36
            if (p_curr->p_right == nullptr)
37
            {
38
                // insert
39
                p_curr->p_right = p_new;
40
                return true;
41
            }
42
            else
43
            {
44
                // keep searching
45
                p_curr = p_curr->p_right;
46
            }
47
        }
48
        else
49
        {
50
            // do not allow duplication
51
            delete p_new;
52
            return false;
53
        }
54
    }
55
}
56

57
bool bstree::search(const int val) const
58
{
59
    node *p_curr = p_root;
60

61
    while (p_curr)
62
    {
63
        if (val < p_curr->data)
64
        {
65
            // keep searching
66
            p_curr = p_curr->p_left;
67
        }
68
        else if (val > p_curr->data)
69
        {
70
            // keep searching
71
            p_curr = p_curr->p_left;
72
        }
73
        else
74
        {
75
            // found
76
            return true;
77
        }
78
    }
79

80
    return false;
81
}
82

83
void bstree::preorder() const
84
{
85
    if (p_root == nullptr)
86
    {
87
        return;
88
    }
89
    
90
    std::stack<node *> s;
91
    s.push(p_root);
92

93
    while (!s.empty())
94
    {
95
        node *p_curr = s.top();
96
        s.pop();
97
        std::cout << p_curr->data << " ";
98

99
        if (p_curr->p_right)
100
        {
101
            s.push(p_curr->p_right);
102
        }
103

104
        if (p_curr->p_left)
105
        {
106
            s.push(p_curr->p_left);
107
        }
108
    }
109

110
    std::cout << std::endl;
111
}
112

113
void bstree::inorder() const
114
{
115
    if (p_root == nullptr)
116
    {
117
        return;
118
    }
119

120
    std::stack<node *> s;
121
    node *p_curr = p_root;
122

123
    while (p_curr || !s.empty())
124
    {
125
        while (p_curr)
126
        {
127
            s.push(p_curr);
128
            p_curr = p_curr->p_left;
129
        }
130

131
        p_curr = s.top();
132
        s.pop();
133
        std::cout << p_curr->data << " ";
134
        p_curr = p_curr->p_right;
135
    }
136

137
    std::cout << std::endl;
138
}
139

140
void bstree::postorder() const
141
{
142
    if (p_root == nullptr)
143
    {
144
        return;
145
    }
146

147
    std::stack<node *> s1, s2;
148
    s1.push(p_root);
149

150
    while (!s1.empty())
151
    {
152
        node *p_curr = s1.top();
153
        s1.pop();
154
        s2.push(p_curr);
155

156
        if (p_curr->p_left)
157
        {
158
            s1.push(p_curr->p_left);
159
        }
160

161
        if (p_curr->p_right)
162
        {
163
            s1.push(p_curr->p_right);
164
        }
165
    }
166

167
    while (!s2.empty())
168
    {
169
        std::cout << s2.top()->data << " ";
170
        s2.pop();
171
    }
172

173
    std::cout << std::endl;
174
}
175

176
bool bstree::remove(const int val)
177
{
178
    node *p_del = p_root;
179
    node *p_del_parent = nullptr;
180

181
    // find a node to delete
182
    while (p_del && p_del->data != val)
183
    {
184
        p_del_parent = p_del;
185
        p_del = (val < p_del->data) ? p_del->p_left : p_del->p_right;
186
    }
187

188
    // node not found
189
    if (p_del == nullptr)
190
    {
191
        return false;
192
    }
193

194
    // case 1: del node has 0 or 1 child
195
    if (p_del->p_left == nullptr || p_del->p_right == nullptr)
196
    {
197
        node *p_del_child = p_del->p_left ? p_del->p_left : p_del->p_right;
198

199
        if (p_del_parent == nullptr)
200
        {
201
            // prepare to delete root
202
            p_root = p_del_child;
203
        }
204
        else if (p_del == p_del_parent->p_left)
205
        {
206
            p_del_parent->p_left = p_del_child;
207
        }
208
        else
209
        {
210
            p_del_parent->p_right = p_del_child;
211
        }
212

213
        delete p_del;
214
        return true;
215
    }
216
    // case 2: del node has 2 children
217
    else
218
    {
219
        // replacement node can be either of the following:
220
        // - largest (right-most) node in the left subtree
221
        // - smallest (leftmost) node in the right subtree
222
        
223
        node *p_rep_parent = p_del;
224
        node *p_rep = p_del->p_left; // finding rep node from left subtree
225

226
        while (p_rep->p_right)
227
        {
228
            p_rep_parent = p_rep;
229
            p_rep = p_rep->p_right;
230
        }
231

232
        // replace del node's data with rep node's
233
        p_del->data = p_rep->data;
234

235
        // delete the rep node
236
        node *p_rep_child = p_rep->p_left; // rep node has no right child
237

238
        if (p_rep == p_rep_parent->p_right)
239
        {
240
            p_rep_parent->p_right = p_rep_child;
241
        }
242
        else
243
        {
244
            p_rep_parent->p_left = p_rep_child;
245
        }
246

247
        delete p_rep;
248
        return true;
249
    }
250
}
251

252
void bstree::clear()
253
{
254
    if (p_root == nullptr)
255
    {
256
        return;
257
    }
258

259
    std::stack<node *> s;
260
    s.push(p_root);
261

262
    // deleting node -> right -> left
263
    while (!s.empty())
264
    {
265
        node *p_curr = s.top();
266
        s.pop();
267

268
        if (p_curr->p_left)
269
        {
270
            s.push(p_curr->p_left);
271
        }
272
        
273
        if (p_curr->p_right)
274
        {
275
            s.push(p_curr->p_right);
276
        }
277

278
        delete p_curr;
279
    }
280

281
    p_root = nullptr;
282
}

Test Driver

51
1
#include <iostream>
2
#include "bstree.hpp"
3

4
int main(int argc, char *argv[])
5
{
6
    bstree bst;
7

8
    // Insert a mix of values
9
    int values[] = {50, 30, 70, 20, 40, 60, 80, 65, 75, 85};
10

11
    for (int val : values) {
12
        bst.insert(val);
13
    }
14

15
    std::cout << "In-order traversal (should be sorted):\n";
16
    bst.inorder();  // 20 30 40 50 60 65 70 75 80 85
17

18
    std::cout << "Pre-order traversal:\n";
19
    bst.preorder(); // 50 30 20 40 70 60 65 80 75 85
20

21
    std::cout << "Post-order traversal:\n";
22
    bst.postorder(); // 20 40 30 65 60 75 85 80 70 50
23

24
    // Search for a few elements
25
    std::cout << "Search 65: " << (bst.search(65) ? "Found" : "Not Found")
26
        << "\n"; // Found
27
    std::cout << "Search 100: " << (bst.search(100) ? "Found" : "Not Found")
28
        << "\n"; // Not Found
29

30
    // Delete a leaf node
31
    bst.remove(20);
32
    std::cout << "After deleting 20 (leaf):\n";
33
    bst.inorder();  // 30 40 50 60 65 70 75 80 85
34

35
    // Delete a node with one child
36
    bst.remove(60);
37
    std::cout << "After deleting 60 (one child):\n";
38
    bst.inorder();  // 30 40 50 65 70 75 80 85
39

40
    // Delete a node with two children
41
    bst.remove(70);
42
    std::cout << "After deleting 70 (two children):\n";
43
    bst.inorder();  // 30 40 50 65 75 80 85
44

45
    // Clear the b
46
    bst.clear();
47
    std::cout << "After clear():\n";
48
    bst.inorder();  // (nothing)
49

50
    return 0;
51
}

15
1
In-order traversal (should be sorted):
2
20 30 40 50 60 65 70 75 80 85
3
Pre-order traversal:
4
50 30 20 40 70 60 65 80 75 85
5
Post-order traversal:
6
20 40 30 65 60 75 85 80 70 50
7
Search 65: Not Found
8
Search 100: Not Found
9
After deleting 20 (leaf):
10
30 40 50 60 65 70 75 80 85
11
After deleting 60 (one child):
12
30 40 50 65 70 75 80 85
13
After deleting 70 (two children):
14
30 40 50 65 75 80 85
15
After clear():