Home | Projects | Notes > Data Structures & Algorithms > Trees
Trees
Terminology
| Term | Definition |
|---|---|
| Node | A basic unit containing data and links to child nodes. |
| Root | The topmost node of the tree; has no parent. |
| Parent | A node that has one or more child nodes. |
| Child | A node that descends from another node. |
| Leaf | A node with no children. |
| Internal Node | A node with at least one child (i.e. not a leaf). Root is also an internal node. |
| Edge | A connection between a parent and a child node. |
| Path | A sequence of nodes connected by edges. |
| Height | The number of edges on the longest path from a node to a leaf. |
| Depth | The number of edges from the root to a node. |
| Level | The depth of a node plus one (root is at level 1). |
| Subtree | A tree formed from any node and its descendants. |
| Sibling | Nodes that share the same parent. |
| Degree | The number of children a node has. |
| Balanced Tree | A tree where the height difference between subtrees is minimal. |
| Binary Tree | A tree where each node has at most two children (left and right). |
Binary Trees
A binary tree is a hierarchical data structure where each node has at most two children: a left child and a right child. It is commonly used to represent structured data like arithmetic expressions, hierarchical relationships, and is the foundation of many search and sorting algorithms.
Common Types
Full binary tree
Every node has 0 or 2 children.
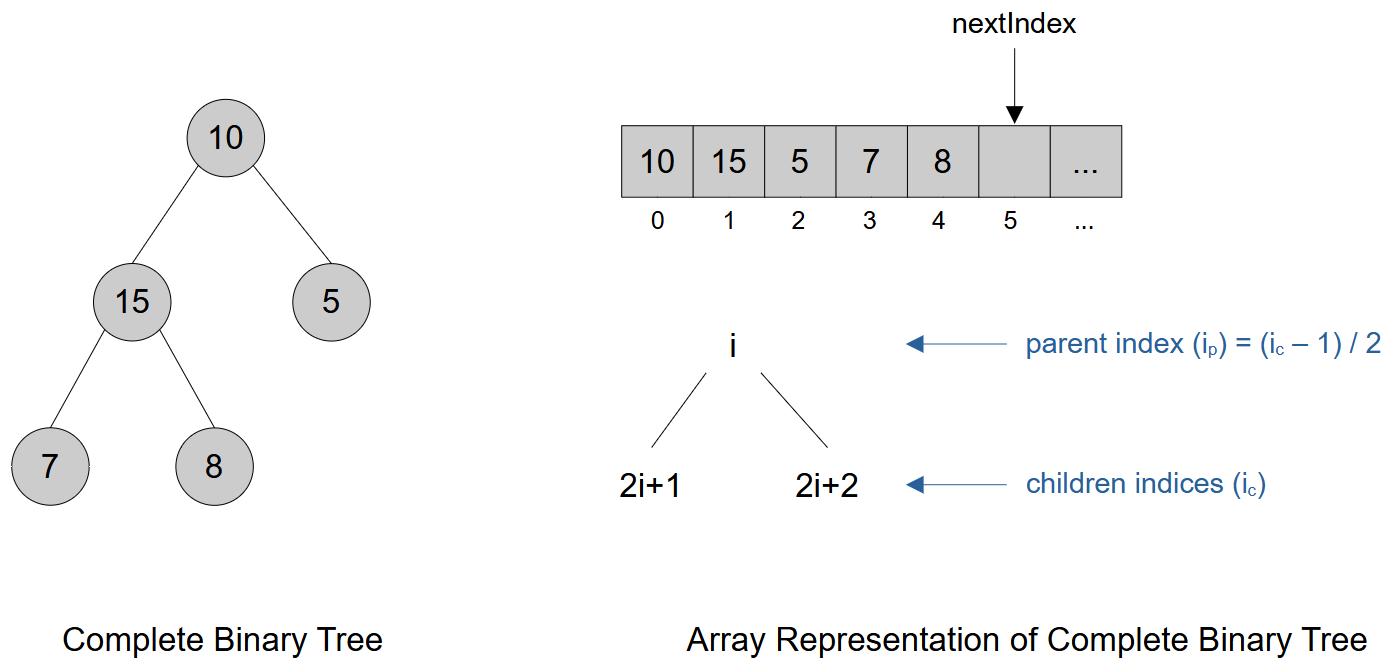
Complete binary tree
All levels are filled except possibly the last, which is filled left to right with no missing nodes.
Not "perfect" since the bottom level is not filled all the way across.
Perfect binary tree
All internal nodes have 2 children, and all leaves are at the same level.
All perfect binary trees are both "complete" and "full"
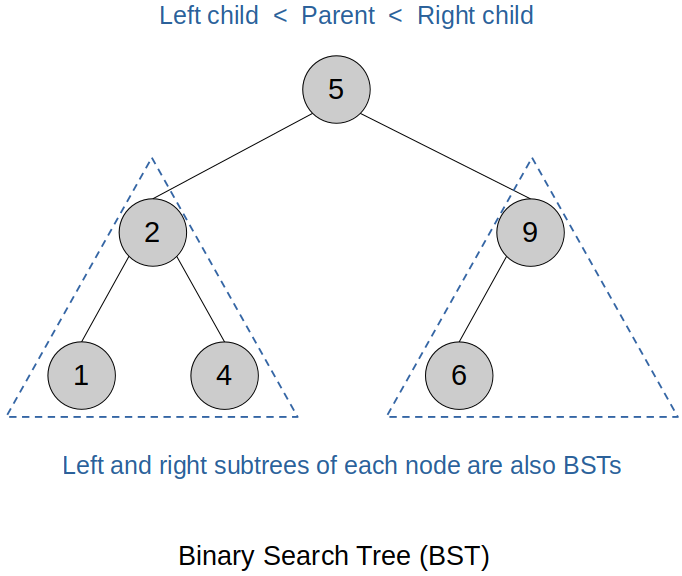
Binary Search Tree (BST)
Left child < parent < right child.
Binary Search Trees
A Binary Search Tree (BST) is a type of binary tree where each node follows a specific ordering rule:
The left subtree contains only nodes with values less than the parent node.
The right subtree contains only nodes with values greater than the parent node.
This rule applies recursively to every subtree in the tree.
BSTs are widely used for efficient searching, insertion, and deletion, with average-case time complexity of O(log n) for balanced trees.
All operations have O(log n) time complexity, which is very efficient. (Every time you go down one level, you are excluding the half of the remaining nodes from your search.)
If a tree never forks, it is essentially a linked list, in which case the search time complexity will be O(n). However, since this is not a general case, a binary search tree is still treated as an O(log n) data structure.